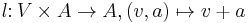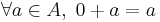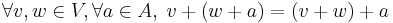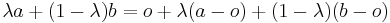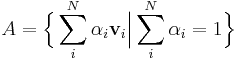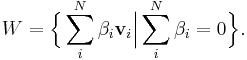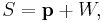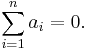Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point that serves as an origin. The solution set of an inhomogeneous linear equation is either empty or an affine space.

1 Informal descriptions
2 Definition
3 Examples
4 Affine subspaces
5 Affine combinations and affine dependence
6 Axioms
7 Relation to projective spaces
8 See also
9 Notes
10 References

Informal descriptions

The following characterization may be easier to understand than the usual formal definition: an affine space is what is left of a vector space after you've forgotten which point is the origin (or, in the words of the French mathematician Marcel Berger, "An affine space is nothing more than a vector space whose origin we try to forget about, by adding translations to the linear maps").^[1] Imagine that Alice knows that a certain point is the true origin, and Bob believes that another point — call it p — is the origin. Two vectors, a and b, are to be added. Bob draws an arrow from p to a and another arrow from p to b, and completes the parallelogram to find what Bob thinks is a + b, but Alice knows that it is actually

p + (a − p) + (b − p).

Similarly, Alice and Bob may evaluate any linear combination of a and b, or of any finite set of vectors, and will generally get different answers. However, if the sum of the coefficients in a linear combination is 1, then Alice and Bob will arrive at the same answer.

If Alice travels to

λa + (1 − λ)b

then Bob can similarly travel to

p + λ(a − p) + (1 − λ)(b − p) = λa + (1 − λ)b.

Then, for all coefficients λ + (1 − λ) = 1, Alice and Bob describe the same point with the same linear combination, starting from different origins.

Here is the punch line: Alice knows the "linear structure", but both Alice and Bob know the "affine structure"—i.e. the values of affine combinations, defined as linear combinations in which the sum of the coefficients is 1. An underlying set with an affine structure is an affine space.

Definition

An affine space is a set 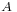$\scriptstyle A$ together with a vector space 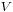$\scriptstyle V$ and a group action of 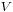$\scriptstyle V$ (with addition of vectors as group operation) on 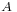$\scriptstyle A$ , such that the only vector acting with a fixpoint is 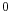$\scriptstyle 0$ (i.e., the action is free) and there is a single orbit (the action is transitive). In other words, an affine space is a principal homogeneous space over the additive group of a vector space.

Explicitly, an affine space is a point set 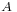$\scriptstyle A$ together with a map

$l\colon V \times A \to A, (v, a) \mapsto v %2B a$

with the following properties:

Left identity

$\forall a \in A,\; 0 %2B a = a$
Associativity

$\forall v, w \in V, \forall a \in A,\; v %2B (w %2B a) = (v %2B w) %2B a$
Uniqueness

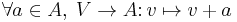$\forall a \in A,\; V \to A\colon v \mapsto v %2B a\quad$ is a bijection.

The vector space 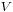$\scriptstyle V$ is said to underlie the affine space 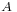$\scriptstyle A$ and is also called the difference space.

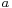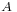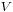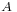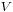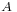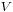By choosing an origin, $\scriptstyle a$ , one can thus identify $\scriptstyle A$ with $\scriptstyle V$ , hence turn $\scriptstyle A$ into a vector space. Conversely, any vector space, $\scriptstyle V$ , is an affine space over itself. The uniqueness property ensures that subtraction of any two elements of $\scriptstyle A$ is well defined, producing a vector of $\scriptstyle V$ .

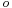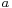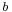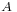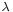If $\scriptstyle o$ , $\scriptstyle a$ , and $\scriptstyle b$ are points in $\scriptstyle A$ and $\scriptstyle\lambda$ is a scalar, then

$\lambda a %2B (1 - \lambda)b = o %2B \lambda (a - o) %2B (1 - \lambda)(b - o)$

is independent of 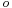$\scriptstyle o$ . Instead of arbitrary linear combinations, only such affine combinations of points have meaning.

By noting that one can define subtraction of points of an affine space as follows:

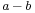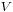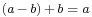$\scriptstyle a \,-\, b$ is the unique vector in $\scriptstyle V$ such that $\scriptstyle \left(a \,-\, b\right) \,%2B\, b \;=\; a$ ,

one can equivalently define an affine space as a point set 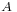$\scriptstyle A$ , together with a vector space 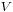$\scriptstyle V$ , and a subtraction map 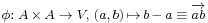$\scriptstyle\operatorname{\phi}:\; A \,\times\, A \;\to\; V,\; \left(a,\, b\right) \,\mapsto\, b \,-\, a \;\equiv\; \overrightarrow{ab}$ with the following properties ^[2]:

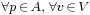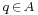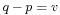$\scriptstyle \forall p \,\in\, A,\; \forall v \,\in\, V$ there is a unique point $\scriptstyle q \,\in\, A$ such that $\scriptstyle q \,-\, p \;=\; v$ and
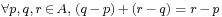$\scriptstyle \forall p,\, q,\, r \,\in\, A,\; (q \,-\, p) \,%2B\, (r \,-\, q) \;=\; r \,-\, p$ .

These two properties are called Weyl's axioms.

Examples

When children find the answers to sums such as 4+3 or 4−2 by counting right or left on a number line, they are treating the number line as a one-dimensional affine space.
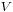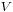Any coset of a subspace $\scriptstyle V$ of a vector space is an affine space over $\scriptstyle V$ .
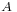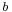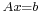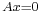If $\scriptstyle A$ is a matrix and $\scriptstyle b$ lies in its column space, the set of solutions of the equation $\scriptstyle Ax = b$ is an affine space over the subspace of solutions of $\scriptstyle Ax = 0$ .
The solutions of an inhomogeneous linear differential equation form an affine space over the solutions of the corresponding homogeneous linear equation.
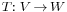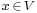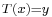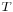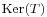Generalizing all of the above, if $\scriptstyle T\colon\; V \,\to\, W$ is a linear mapping and y lies in its image, the set of solutions $\scriptstyle x \,\in\, V$ to the equation $\scriptstyle T(x) = y$ is a coset of the kernel of $\scriptstyle T$ , and is therefore an affine space over $\scriptstyle {\rm Ker}(T)$ .

Affine subspaces

An affine subspace (sometimes called a linear manifold, linear variety, or a flat) of a vector space 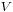$\scriptstyle V$ is a subset closed under affine combinations of vectors in the space. For example, the set

$A=\Bigl\{\sum^N_i \alpha_i \mathbf{v}_i \Big| \sum^N_i\alpha_i=1\Bigr\}$

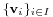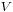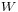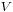
is an affine space, where $\scriptstyle \{ \mathbf{v}_i \}_{i\in I}$ is a family of vectors in $\scriptstyle V$ – this space is the affine span of these points. To see that this is indeed an affine space, observe that this set carries a transitive action of the vector subspace $\scriptstyle W$ of $\scriptstyle V$

$W=\Bigl\{\sum^N_i \beta_i\mathbf{v}_i \Big| \sum^N_i \beta_i=0\Bigr\}.$

This affine subspace can be equivalently described as the coset of the 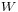$\scriptstyle W$ -action

$S=\mathbf{p}%2BW,\,$

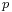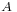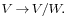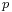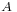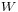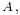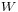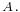
where $\scriptstyle p$ is any element of $\scriptstyle A$ , or equivalently as any level set of the quotient map $\scriptstyle V \,\to\, V/W.$ A choice of $\scriptstyle p$ gives a base point of $\scriptstyle A$ and an identification of $\scriptstyle W$ with $\scriptstyle A\, ,$ but there is no natural choice, nor a natural identification of $\scriptstyle W$ with $\scriptstyle A\, .$

A linear transformation is a function that preserves all linear combinations; an affine transformation is a function that preserves all affine combinations. A linear subspace is an affine subspace containing the origin, or, equivalently, a subspace that is closed under linear combinations.

For example, in 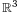$\scriptstyle {\mathbb R^3}$ , the origin, lines and planes through the origin and the whole space are linear subspaces, while points, lines and planes in general as well as the whole space are the affine subspaces.

Affine combinations and affine dependence

Main article: Affine combination

An affine combination is a linear combination in which the sum of the coefficients is 1. Just as members of a set of vectors are linearly independent if none is a linear combination of the others, so also they are affinely independent if none is an affine combination of the others. The set of linear combinations of a set of vectors is their "linear span" and is always a linear subspace; the set of all affine combinations is their "affine span" and is always an affine subspace. For example, the affine span of a set of two points is the line that contains both; the affine span of a set of three non-collinear points is the plane that contains all three.

Vectors

v₁, v₂, ..., v_n

are linearly dependent if there exist scalars a₁, a₂, …,a_n, not all zero, for which

a₁v₁ + a₂v₂ + … + a_nv_n = 0

(1)

Similarly they are affinely dependent if in addition the sum of coefficients is zero:

$\sum_{i=1}^n a_i = 0.$

Axioms

Affine space is usually studied as analytic geometry using coordinates, or equivalently vector spaces. It can also be studied as synthetic geometry by writing down axioms, though this approach is much less common. There are several different systems of axioms for affine space.

Coxeter (1969, p.192) axiomatizes affine geometry (over the reals) as ordered geometry together with an affine form of Desargues's theorem and an axiom stating that in a plane there is at most one line through a given point not meeting a given line.

Affine planes satisfy the following axioms (Cameron 1991, chapter 2): (in which two lines are called parallel if they are equal or disjoint):

Any two distinct points lie on a unique line.
Given a point and line there is a unique line which contains the point and is parallel to the line
There exist three non-collinear points.

As well as affine planes over fields (or division rings), there are also many non-Desarguesian planes satisfying these axioms. (Cameron 1991, chapter 3) gives axioms for higher dimensional affine spaces.

Relation to projective spaces

Affine spaces are subspaces of projective spaces: an affine plane can be obtained from any projective plane by removing a line and all the points on it, and conversely any affine plane can be used to construct a projective plane as a closure by adding a "line at infinity" whose points correspond to equivalence classes of parallel lines.

Further, transformations of projective space that preserve affine space (equivalently, that preserve the points at infinity as a set) yield transformations of affine space, and conversely any affine linear transformation extends uniquely to a projective linear transformations, so affine transformations are a subset of projective transforms. Most familiar is that Möbius transformations (transformations of the projective line, or Riemann sphere) are affine (transformations of the complex plane) if and only if they fix the point at infinity.

However, one cannot take the projectivization of an affine space, so projective spaces are not naturally quotients of affine spaces: one can only take the projectivization of a vector space, since the projective space is lines through a given point, and there is no distinguished point in an affine space. If one chooses a base point (as zero), then an affine space becomes a vector space, which one may then projectivize, but this requires a choice.

Notes

^ Berger, Marcel (1987), p. 32
^ Nomizu, K.; Sasaki, S. (1994), p. 7

References

Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3
Cameron, Peter J. (1991), Projective and polar spaces, QMW Maths Notes, 13, London: Queen Mary and Westfield College School of Mathematical Sciences, MR 1153019, http://www.maths.qmul.ac.uk/~pjc/pps/
Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 123930
Dolgachev, I.V.; Shirokov, A.P. (2001), "Affine space", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=A/a011100
Snapper, Ernst; Troyer, Robert J. (1989), Metric Affine Geometry (Dover edition, first published in 1989 ed.), Dover Publications, ISBN 0-486-66108-3
Nomizu, K.; Sasaki, S. (1994), Affine Differential Geometry (New ed.), Cambridge University Press, ISBN 978-0-521-44177-3